Skip to main content

Section 1 Math 140 Problems

Students entering Math 140 should be able to successfuly complete the problems below.

Exercises Exercises

1.

If \(f(x)=16x-x^2\text{,}\) what is the area of the rectangle \(A\text{?}\)

Solution.

The area is length times height, so

\begin{equation*} f(4)\cdot 4 = (16(4)-4^2)\cdot 4 = (64-16)\cdot 4 = 192 \end{equation*}
2.

Let \(h(x)=e^{3x+7}\text{.}\) Find functions \(f\) and \(g\) so that \(h(x)=f(g(x))\text{.}\)

Solution.

Set \(f(x)=e^x\) and \(g(x)=3x+7\text{.}\)

3.

Let \(C=f(A)\) be the cost in dollars of purchasing a plot of land of area \(A\) square feet. What do the quantities \(f(5000)\) and \(f^{-1}(250,000)\) represent?

Solution.

The quantity \(f(5000)\) is the cost (in dollars) of purchasing a plot of land of area \(5000\) square feet.

The quantity \(f^{-1}(250,000)\) is the area (in square feet) of a plot of land that you can purchase for \(250,000\) dollars.

4.

Let \(f(x)=\dfrac{x^3-9x}{2x^3-6x^2}\text{.}\)

  1. Identify the locations of the discontinuities of \(f(x)\) and classify them as holes or the location of a vertical asymptote.

  2. Analyze the end behavior of \(f\text{.}\) That is, what happens as \(x\) goes towards \(\infty\) or \(-\infty\text{?}\)

Solution.

  1. First factor the denominator of \(f(x)\text{:}\)

    \begin{equation*} 2x^3-6x^2=2x^2(x-3)\text{.} \end{equation*}

    The denominator equals \(0\) when \(x=0\) or \(x=3\text{,}\) so those are the locations of the discontinuities.

    To classify them, we factor the numerator as well and cancel where possible:

    \begin{equation*} x^3-9x=x(x^2-9)=x(x-3)(x+3)\text{.} \end{equation*}

    So

    \begin{equation*} \frac{x(x-3)(x+3)}{2x^2(x-3)}=\frac{x+3}{2x}\text{.} \end{equation*}

    Since \(x-3\) is no longer in the denominator after canceling, \(x=3\) is a hole in the graph. Since \(x\) is still in the denominator, \(x=0\) is a vertical asymptote of the graph.

  2. In the long run, \(f\) behaves like \(y=\dfrac{x^3}{2x^3}=\dfrac{1}{2}\text{.}\) That is, the graph has a horizontal asymptote of \(y=\frac{1}{2}\) to both the left and right.

5.

The enrollment at JU is given by the following graph of a linear function, where \(S\) represents the number of students and \(t\) represents the number of years since the year \(2000\text{.}\)

  1. Using the two given points on the graph, determine the rate of change (slope) of the linear function.

  2. How many students were there in the year \(2000\text{?}\)

  3. Determine a formula for \(S\) as a function of \(t\text{.}\)

Solution.

  1. The slope is found by computing rise over run using the given points:

    \begin{equation*} \text{slope} = \frac{2744-2636}{4-1} = \frac{108}{3} = 36\text{.} \end{equation*}

  2. The year \(2000\) corresponds to \(t=0\text{,}\) so we want the \(S\)-intercept of the line, which is \(2600\) students.

  3. We know the slope and intercept of the line, so we use slope-intercept form: \(S(t) = 36t + 2600\text{.}\)

6.

Without using a calculator, match each formula to a graph.

  1. \(\displaystyle P=20(1.02)^t\)

  2. \(\displaystyle P=20(0.98)^t\)

  3. \(\displaystyle P=20(0.96)^t\)

  4. \(\displaystyle P=20(1.04)^t\)

Solution.

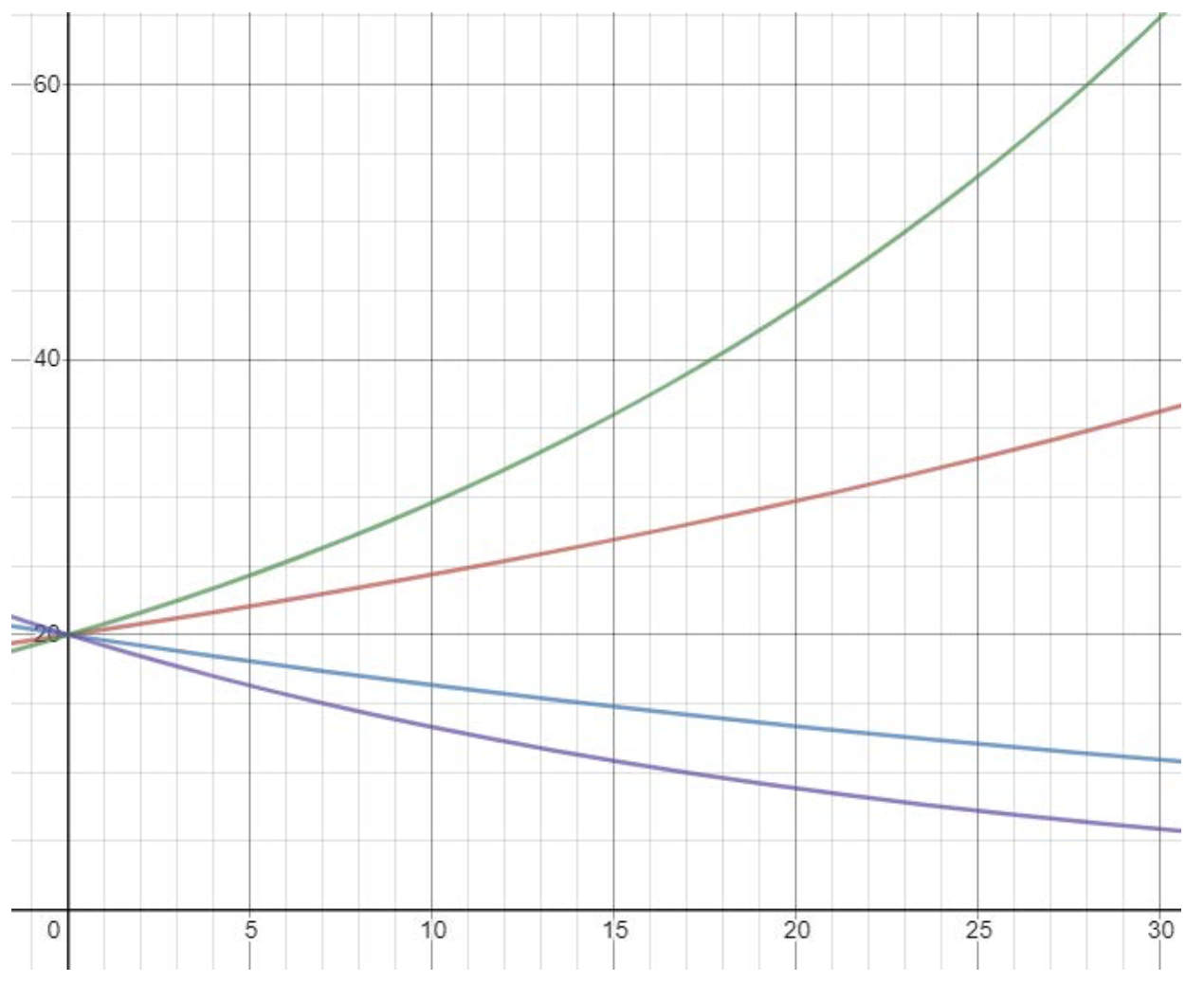
From top to bottom, the graphs are (d), (a), (b), (c).

7.

Suppose the population of a certain small country is given by \(P(t)=19.5e^{0.01t}\text{,}\) where \(P\) is the population in millions, \(t\) years after the year \(2000\text{.}\) Calculate and describe the meaning of \(P(8)\text{.}\) Include units in your answer.

Solution.
\begin{equation*} P(8)=19.5e^{0.01(8)}\approx 43.398 \text{ million people} \end{equation*}

This means that in the year 2008, the population of the small country was approximately \(43.398\) million people (\(43,398,000\) people).

8.

The rabbit population in a national park rises and falls each year. The population is at its minimum number of rabbits at the beginning of January and increases in size to its maximum at the beginning of July. The population \(P\) of rabbits (in thousands) \(t\) months after January 1 is given by

\begin{equation*} P(t)=-5\cos\left(\frac{\pi}{6}t\right) + 10\text{.} \end{equation*}

What is the maximum population of rabbits each year? What is the minimum population of rabbits each year?

Solution.

The maximum population is at the beginning of July, which is \(t=6\text{:}\)

\begin{equation*} P(6) = -5\cos\left(\frac{\pi}{6} \cdot 6 \right) + 10 = -5(-1) +10 = 15 \text{ thousand rabbits}\text{.} \end{equation*}

The minimum population is at the beginning of January, which is \(t=0\text{:}\)

\begin{equation*} P(0) = -5\cos\left(\frac{\pi}{6} \cdot 0 \right) + 10 = -5(1) +10 = 5 \text{ thousand rabbits} \end{equation*}
9.

Fully simplify the expression \(\dfrac{\sin^2(x)}{\tan^2(x)} + \tan^2(x)\cos^2(x)\text{.}\)

Solution.

Since \(\tan(x)=\dfrac{\sin(x)}{\cos(x)}\text{,}\) we have

\begin{align*} \frac{\sin^2(x)}{\tan^2(x)} \amp = \sin^2(x) \cdot \frac{1}{\tan^2(x)}\\ \amp = \sin^2(x) \cdot \frac{\cos^2(x)}{\sin^2(x)}\\ \amp = \cos^2(x) \end{align*}

and

\begin{align*} \tan^2(x) \cos^2(x) \amp = \frac{\sin^2(x)}{\cos^2(x)}\cos^2(x)\\ \amp = \sin^2(x)\text{.} \end{align*}

So

\begin{equation*} \frac{\sin^2(x)}{\tan^2(x)} + \tan^2(x)\cos^2(x) = \cos^2(x) +\sin^2(x) =1\text{.} \end{equation*}