Skip to main content

Section 2 Core-Level Math Classes Problems

Students entering a Core-level Math class should be able to successfuly complete the problems below.

Exercises Exercises

1.

Fully simplify the following expressions:

  1. \(\displaystyle ((2t)^5)^3\)

  2. \(\displaystyle ((-g)^4)^4\)

  3. \(\displaystyle (6m^2n^{-1})^3\)

  4. \(\displaystyle \dfrac{(3w^2)^5}{(6w^{-2})^2}\)

  5. \(\displaystyle \dfrac{2x^2}{10x^7}\)

Solution.

  1. \(\displaystyle ((2t)^5)^3 = 2^{5\cdot 3} \cdot t^{5\cdot 3} = 2^{15} t^{15}= 32768 t^{15}\)

  2. \(\displaystyle ((-g)^4)^4 = (-g)^{4\cdot 4} = g^{16}\)

  3. \(\displaystyle (6m^2n^{-1})^3 = 6^3 m^{(2\cdot3)}n^{(-1\cdot 3)}= \dfrac{6^3m^6}{n^3}= \dfrac{216m^6}{n^3}\)

  4. \(\displaystyle \dfrac{(3w^2)^5}{(6w^{-2})^2}= \dfrac{3^5w^{2\cdot 5}}{6^2w^{(-2\cdot 2)}} = \dfrac{3^5w^{10}}{6^2w^{-4}} = \dfrac{3^5w^{10}w^{4}}{6^2} = \dfrac{27w^{14}}{4}\)

  5. \(\displaystyle \dfrac{2x^2}{10x^7} = \dfrac{1}{5x^5}\)

2.

  1. Simplify the expression \(2(3x^2-8)-5x^2\text{.}\)

  2. Solve \(2(3x^2-8)-5x^2=0\) for \(x\text{.}\)

Solution.

  1. \(2(3x^2-8)-5x^2 = 6x^2-16-5x^2=x^2-16\text{.}\)

  2. \begin{gather*} x^2-16 = 0\\ (x-4)(x+4)=0\\ x=4 \text{ or } x=-4 \end{gather*}

3.

The sophomore class of two different schools were surveyed. The following results show the declared majors.

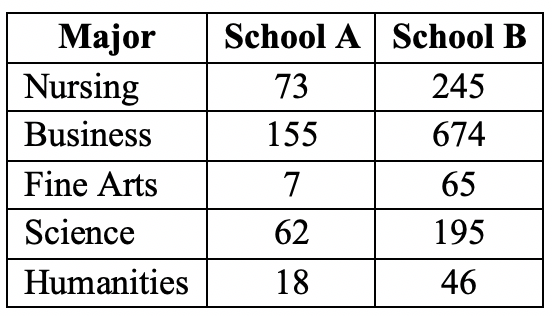
  1. What percentage of sophomore students in School A major in Business?

  2. Which school has a higher percentage of sophomore students who major in Nursing?

Solution.

  1. The total number of sophomore students in School A is \(315\text{.}\) So the fraction majoring in business is \(\dfrac{155}{315}=0.492\) and the percentage is \(49.2\%\text{.}\)

  2. School A has \(315\) students and School B has \(1225\) students.

    School A Nursing percentage: \(\dfrac{73}{315} \cdot 100 \% = 23.2 \%\)

    School B Nursing percentage: \(\dfrac{245}{1225}\cdot 100 \% = 20 \%\)

    So School A has a higher percentage of sophomore students who major in Nursing.

4.

Find an equation for the line passing through the points \((-2,5)\) and \((4,-3)\text{.}\)

Solution.

We first find the slope of the line, which is

\begin{equation*} m=\frac{-3-5}{4-(-2)}= \frac{-8}{6}=-\frac{4}{3}\text{.} \end{equation*}

Using point-slope form with the point \((-2,5)\) and the slope \(m=-\dfrac{4}{3}\text{,}\) the line has equation

\begin{equation*} y-5=-\frac{4}{3}(x+2)\text{.} \end{equation*}

Additional correct answers include \(y+3=-\frac{4}{3}(x-4)\) and \(y=-\frac{4}{3}x+\frac{7}{3}\text{.}\)